When it comes down to real time computer graphics, shadows rendering is one of the hottest topics. Shadow maps are currently the most used shadowing technique: they are reasonably fast, simple to implement (in their basic incarnations at least!) and unlike stencil shadows, they work even with not manifold meshes. Unfortunately shadow maps can look ugly as well, their resolution is never enough and all those aliasing and ‘acne’ problems drive people insane. This is why every year a lot of research goes into new shadowing techniques or into improving current ones. Papers and articles about shadow mapping often divide into two distinct groups:
- How to improve virtual shadow maps resolution ( for example all the works about warped projection schemes belong to this category ).
- How to improve shadow maps filtering quality/speed for hard edged and/or soft edged shadows
Personally, I find this second class of problems more interesting, cause it is still unknown territory and there is a lot of work to do about it.
A popular shadow maps filtering algorithm is percentage closer filtering, first developed by Pixar and later integrated by NVIDIA on their graphics hardware. It is based on taking a number of samples (the more, the better..) from a shadow map, performing a depth test with each of them against a shadow receiver and then averaging together all the depth test results.The key idea here is that filtering a shadow map, unlike what we do with colour textures, is not about directly filtering a bunch of depth values.Averaging together depth values and performing a single depth test on their mean value wouldn’t make any sense, cause a group of occluders which are not spatially correlated can’t be represented by a single averaged occluder. That’s why to have meaningful results filtering has to happen after depth tests, not before.
PCF is still the most used technique to filter shadow maps but a new algorithm called Variance Shadow Maps (developed by William Donnelly and Andrew Lauritzen) has deservedly attracted a lot of attention. VSM are based on a somewhat different and extremely interesting approach: depth values located around some point over a shadow map are seen as a discrete probability distribution. If we want to know if a receiver is occluded by this group of depth samples we don’t need to perform many depth tests anymore, we just want to know the probability of our receiver to be occluded or not. Constructing on the fly a representation of an unknown (a priori) discrete probability distribution it is basically an impossible task, so Donnelly and Lauritzen’s method doesn’t try to compute the exact probablity of being in shadow.
Chebyshev’s inequality is used instead to calculate an upper bound for this probability. This inequality categorizes a probability distribution using only two numbers: mean and variance, which can be easily computed per shadow map texel. Incidentally what we need to do in order to compute mean and variance is similar to what we do when we filter an image. So this new approach allows for the first time to filter shadow maps in light space as we do with colour images, and also enable us to use GPUs hardwired texture filtering capabilities to filter a variance shadow map.
No wonder VSM triggered a lot of interest (a rapidly growing number of games is using this new techinque) as it has made possible what many, me included, thought was not possible. We can now apply filters to the variance shadow map and work with it as we were working with some colour texture. Here an example of the kind of high quality shadow that is possible to achieve filtering a variance shadow map with a 7×7 taps gaussian filter. In this case filtering has been applied with a separable filter so that we just need to work on 2N samples per shadow map texel instead of NxN samples that PCF would require.

Variance Shadow Maps – 7×7 Gaussian Filter
Memory requirements and hardware filtering issues aside VSM only significant flaw is light bleeding/leaking: a problem that manifests itself when shadows casted by occluders that are not relatively close to each other overlap over the same receiver.
For example in this screen shot a triangle (not visibile in the image) located above the teapot is casting a shadow over the rest of the scene, and we can easily tell the shape of this new occluder by the lighter areas that are now inside the shadow casted by the teapot.

Variance Shadow Maps – Light bleeding caused by a second occluder
Occluders that overlap within a filtering region and that are not close to each other generate high depth variance values in the variance shadow map. High variance deteriorates the quality of the upper bound given by Chebyshev’s inequality, and since this inequality performs a conservative depth test, it can’t simply tell us if a point is in shadow or not. The amount of light leaking into shadows is directly proportional to the filter kernel size; this is what we get using a wider filter:

Variance Shadow Maps – More light bleeding with a 15×15 Gaussian Filter
A well known work around for this issue is to over darken the occlusion term computed via Chebyshev’s inequality in order to reduce areas affected by light leaks. Over darkening can be achieved via 1D textures look-ups that encode a pre-defined and artist-controlled monotonic decreasing function or we can explicitly use functions such as 
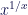
This method doesn’t guarantee to eliminate light bleeding cause variance can’t really be bound in the general case (think about a mountain casting a shadow over a little town). Over darkening also destroy high frequency information in shadow silhouettes, at an extent that can transform high quality shadows in undefined dark blobs, which can be a nice side-effect in those applications where we are not trying to produce realistic shadows!
When I first found out about variance shadow maps I was so excited about this new way to address shadow maps filtering that I thought there must have been a way to improve this technique in order to reduce light leaks without resorting to over darkening. It is obvious that Chebyshev’s inequality is in some cases failing to produce a good upper bound for an occlusion term cause it has not enough information to work with. The first and the second raw moments are not sufficient to describe a probability distribution, in fact is fairly easy to construct whole families of distributions that generate the same first and second order moments! This is a clear case of bad lossy compression: we discarded too much information and now we realize more data are necessary to describe our depth distribution.
At the beginning the solution seemed so simple to me: two moments are not enough and higher order moments need to be accounted for.How many of them? I didn’t know.. but I also quickly realized that computing higher order moments and deriving any other quantity from them (skewness, kurtosis, etc..) is an extremely difficult task due to numerical issues.
There is also another problem to solve, and not a simple one by any mean. What are we going to do with the extra moments? how do we evaluate the probability of being in shadow? I couldn’t find in statistics and probability theory literature any inequality that could handle an arbitrary number of moments. Moreover even though inequalities that handle three or four moments exist, they are mathematical monsters and we don’t want to evaluate them on a per pixel basis. In the end I decided to give it a go only to find out that this incredibly slow and inaccurate extension to variance shadow maps was only marginally improving light bleeding problems, and in some cases the original technique was looking better anyway due to good numerical stability that was sadly lacking in my own implementation.
Having found myself in a cul de sac I tried something completely different such as defining ‘a priori’ the shape of the (not anymore) unknown depth distribution. The shape of this new object is controlled by a few parameters that can be determined fitting per pixel its raw moments to the moments of the real depth distribution. Unfortunately even in this case is extremely difficult to come up with a function that is flexible enojgh to fit any real world distribution and that at the same is not mathematically too complex (we like real time graphics, don’t we?). I ran experiments with a few different models; the most promising one was a 4 parameters model built upon a mixture of 2 gaussian distributions sharing the same variance but having different mean values. It worked very well when we only have two distinct occluders in the filtering window, but it looked awful everytime something a bit more complex came to play within the filtering window.
Ultimately I had to change direction a third time, going back to a variation of the first method that I previously (and stupidly) discarded without evaluating it. The approach is relatively simple, no monstrous equations involved, and in a very short time I got something up and running:

A new shadow map filtering method
As you can see this image is quite similar to the its counterpart rendered with variance shadow maps. It does not handle not planar receivers as good as VSM (note the shadow casted by the handle over the teapot) but in only requires two or four bytes per shadow map texel to work, as canonic shadow maps implementations. Mip mapping and filters in shadow map space work fine too, but the most relevant advantage of this new technique is that it’s completely light leaks free at overlapping shadows (and no over darkening is required, it just works!). The only observable light bleeding is uniformly diffused and only depends upon the relative distance between casters and receivers. It is completely controllable via a scalar value, so that we can trade sharper (but still anti-aliased) shadow edges for less light leaks.

the malicious triangle is back but light leaks are no more!
Evaluating the occlusion term is also very cheap, it just requires a bunch of math ops and a single (at least bilinear filtered) sample from the shadow map, so that this technique is amenable to be implemented even on not very fast GPUs, as long as they support Shader Model 2.0. Although at this point in time I know why it doesn’t always do an amazing job I still have to find a way to fix the remaining problems without incurring in severe performance degradations. It is also easy to derive a ‘dual’ version of the orignal method that does not exhibit any of the previous issues but it also over darken shadows a bit too much.
I will post more about it in the future adding more information (still trying to improve it!) but all the details about it will be available next February when the sixth iteration of the Shader X books series will ship to bookstores.
equally weighted occluders
and a receiver
is to perform a depth test on all occluders, depth test results are then averaged together to obtain a filtered occlusion term. The are many ways to write
and a limit of exponential functions guarantees a fast convergence:
.
quickly converges to zero for all occluders:
controls the sharpness of our step function approximation and can be used to fake soft shadows. Ultimately we can drop the limit and we obtain the ESM occlusion term formula: